进一步理解函数、极值、导数的概念，能够用Matlab进行正确的仿真并进行实际应用。

能够正确根据具体题目要求进行编程、仿真，具体见内容及说明。

1、单变量函数值的计算和绘图 函数 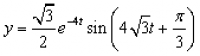要求以0.01 s为间隔，求出y的151个点，并求出其导数的值和曲线。 可以采取下列两种方法来做 1、直接用文本文件中编程的方法(文件名：ex1_1_1.m); 2、编成函数文件，由主程序调用的方法(文件名：ex1_1_2.m，ex1_1_2_f.m); 注：求导数采用diff函数对数组y作运算。

2、参变方程的计算和绘图(摆线的绘制) 当圆轮在平面上滚动时，轮上任一点所画出的轨迹称为摆线。如果这一点不在圆周上而在圆内， 则生成内摆线;如果该点在圆外，即离圆心距离大于半径，则生成外摆线。 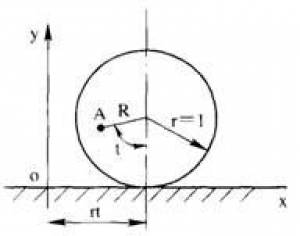其普遍方程可表为：

x = rt - Rsin t
y=r- Rcos t

要求以0.1s为间隔，求出y的101个点，并求出其导数的值和曲线(文件名：ex1_2.m)。

3、曲线族的绘制 对给定的三次曲线方程

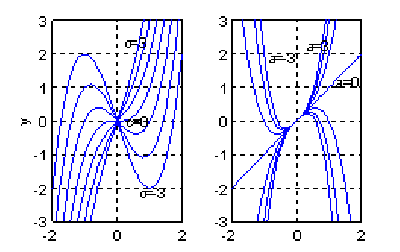
试探讨参数a和c对其图形的影响。 画出c和a取不同值时该函数的曲线族(文件名：ex1_3.m) 注：函数比较简单，可以直接写入绘图语句中，用循环语句来改变参数。注意坐标的设定方法，以得到适于观察的图形，如下图所示： 4、极限的定义和判别 用函数极限的定义对于函数y=f(x)，当任意给定一个正数ε时，有一个对应的正数δ存在，使得当 时 ，则A就是f(x)的极限，如果找不到这样的δ，A就不是它的极限。只考虑左极限，则可以不加绝对值符号。 用以下两个数据尝试判断(文件名：ex1_4.m): （1） f(x)=x^2-8在x→xc=3时是否以1.001为左极限? （2） 在x→xc=0时是否以1为左极限? 对(1)作出的结果将是“左极限不正确”，而对（2）将得出“左极限可能正确”的结果。 注： Eval函数:将括号内的字符串视为语句并运行，如: eval(‘str’) % str代表特定的命令字符串，在matlab主窗口中输入str再运行。 fxc=input(' f(x)的表达式为，例如sin(x)/x:\n'，'s') 输入函数表达式 5、非线性方程求解 用切线法(牛顿法)求任意非线性方程f(x)=0的解，这也可化为求任意曲线y=f(x)过零点的问题。例如用切线法求下列方程的近似数值解

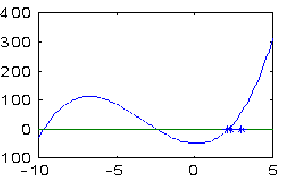
注：可先大致看一下曲线的形状。它有三个过零点。分别在-10，-3，3附近。利用牛顿法编程求解(文件名：ex1_5.m)，示意图如下：

数学基础实验.rar